Solution for Practical 9: Within-family GWAS
Summer Institute of Statical Genetics (Module 15)
2022-07-27
Last updated: 2022-07-27
Checks: 7 0
Knit directory: SISG2022_Association_Mapping/
This reproducible R Markdown analysis was created with workflowr (version 1.7.0). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20220530) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.
The results in this page were generated with repository version 8015362. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.
Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:
Ignored files:
Ignored: analysis/.DS_Store
Ignored: analysis/.Rhistory
Ignored: code/.Rhistory
Ignored: data/.DS_Store
Ignored: lectures/.DS_Store
Untracked files:
Untracked: analysis/.Session07_practical_Key.Rmd.swp
Untracked: analysis/.index.Rmd.swp
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the repository in which changes were made to the R Markdown (analysis/SISGM15_prac9Solution.Rmd) and HTML (docs/SISGM15_prac9Solution.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | 8015362 | Joelle Mbatchou | 2022-07-27 | add key |
This practical can be run in R on your own computer.
This practical aims at illustrating that within-family GWAS are robust to population stratification. We provide a set of R commands below to simulate the phenotypes and genotypes (at \(M=1,000\) SNPs) of \(N=10,000\) independent sibling pairs. Each sibling pair is sampled from \(g\) subgroups, which differ in allele frequencies and mean phenotypes.
None of the \(M\) SNPs is associated with the trait within-each subpopulations. Therefore, the mean association \(\chi^2\) test statistic across SNPs is expected to equal 1. Any deviation reflects population stratification.
The R function CHISQ below returns the mean association \(\chi^2\) test statistic across \(M=1,000\) simulated SNPs for 3 analytical strategies:
simple linear regression using phenotypes and genotypes of the oldest siblings (
X1andY1)same as (1) but fitting 10 genotypic principal components (PC)
within-family GWAS from regressing
Y1-Y2onto colums ofX1-X2
Copy/Run the following command to enable the CHISQ function in your current R environment.
CHISQ <- function(N=10000, # Sample size
M=1000, # Number of SNPs tested
Fst=0.025,# Genetic differentiation between subgroups
vs=.05, # variance explained by stratification
g=2, # Number of subgroups
nPC=10){ # Number of PCs fitted
ms <- rnorm(n=g,mean=0,sd=sqrt(vs))
p <- runif(n=M,min=0.05,max=0.95)
tab <- cut(1:N,breaks = quantile(1:N,probs = seq(0,1,len=g+1)),include.lowest = TRUE)
grp <- as.numeric(tab)
simPS <- function(N,M,Fst,p,g){
a <- p*(1-Fst)/Fst
b <- (1-Fst)*(1-p)/Fst
tab <- cut(1:N,breaks = quantile(1:N,probs = seq(0,1,len=g+1)),include.lowest = TRUE)
grp <- as.numeric(tab)
n <- as.numeric(table(tab))
X <- do.call("rbind",lapply(1:g, function(k){
px <- rbeta(M,shape1=a,shape2=b)
do.call("cbind",lapply(1:M, function(j){
rbinom(n=n[k],size=2,prob=px[j])
}))
}))
return(X)
}
Xm <- simPS(N,M,Fst,p,g) # Simulage genotypes of mother
Xf <- simPS(N,M,Fst,p,g) # Simulate genotyoes of father
X1 <- do.call("cbind",lapply(1:M, function(j){
rbinom(n=N,size=1,prob=Xm[,j]/2) + rbinom(n=N,size=1,prob=Xf[,j]/2)
}))
X2 <- do.call("cbind",lapply(1:M, function(j){
rbinom(n=N,size=1,prob=Xm[,j]/2) + rbinom(n=N,size=1,prob=Xf[,j]/2)
}))
Y1 <- rnorm(n=N,mean=ms[grp],sd=sqrt(1-vs))
Y2 <- rnorm(n=N,mean=ms[grp],sd=sqrt(1-vs))
## PCA
SVD <- svd(scale(X1))
system.time( pcs <- SVD$u )
PC1 <- pcs[,1] * SVD$d[1]
PC2 <- pcs[,2] * SVD$d[2]
plot(PC1,PC2,pch=19,cex=0.5,col=grp,axes=FALSE,
xlab="PC1",ylab="PC2")
axis(1);axis(2)
abline(h=0,v=0,col="grey")
## GWAS
gwas_pop <- do.call("rbind",lapply(1:M, function(j){
summary(lm(Y1~X1[,j]))$coefficients[2,]
}))
gwas_pcs <- do.call("rbind",lapply(1:M, function(j){
summary(lm(Y1~X1[,j] + pcs[,1:nPC]))$coefficients[2,]
}))
gwas_wf <- do.call("rbind",lapply(1:M, function(j){
summary(lm(I(Y1-Y2)~I(X1[,j]-X2[,j])))$coefficients[2,]
}))
ChisqUnAdj <- mean(gwas_pop[,3]^2)
ChisqPCAdj <- mean(gwas_pcs[,3]^2)
ChisqQFAM <- mean(gwas_wf[,3]^2)
return(c(UnAdj=ChisqUnAdj,PCAdj=ChisqPCAdj,QFAM=ChisqQFAM))
} The CHISQ function has 5 input parameters: N (sample size), M (number of SNPs tested), Fst (a parameter measuring genetic differentiation between subgroups in the sample), vs (variance explained by stratification) and g (the number of subgroups in the sample).
Let’s run a first sample with N=10000 individuals, g=2 subgroups in the sample, M=1000 SNPs, Fst=.025 and stratification explaining vs=.05 of the phenotypic variance.
set.seed(27072022)
system.time( testResults <- CHISQ(N=10000,M=1000,Fst=.025,vs=.05,g=2) )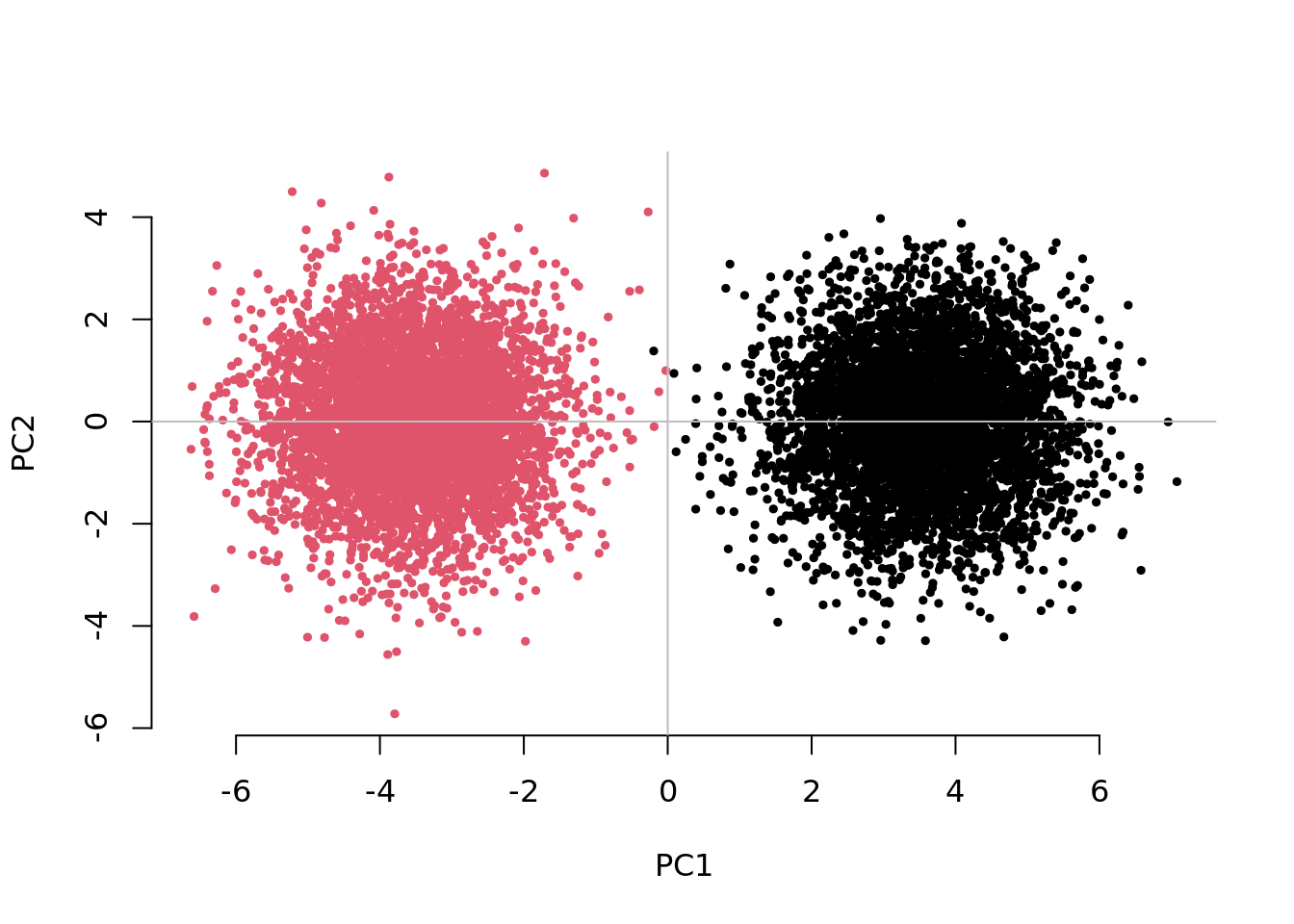
user system elapsed
56.586 0.756 57.346 testResults UnAdj PCAdj QFAM
2.0576085 0.9916819 0.9163870 This example generates a PCA plot (PC1 vs PC2) showing a neat separation between the two subgroups in the sample. In addition, the mean association test statistic for the unadjusted analysis is UnAdj~2.0, which indicates confounding due to population stratification given that none of these SNPS are associated with the phenotype. Note that the mean association test statistic is reduced to PCAdj~1.0, when adjusting these analyses for 10 PCs and to ChisqQFAM~0.9 for the within-family GWAS.
Question 1. Change the seed number (check the set.seed() function above) and run the previous command (CHISQ(N=10000,M=1000,Fst=.025,vs=.05,g=2)) in your own environment. Do you find consistent observations?
set.seed(22061986)
system.time( testResults <- CHISQ(N=10000,M=1000,Fst=.025,vs=.05,g=2) )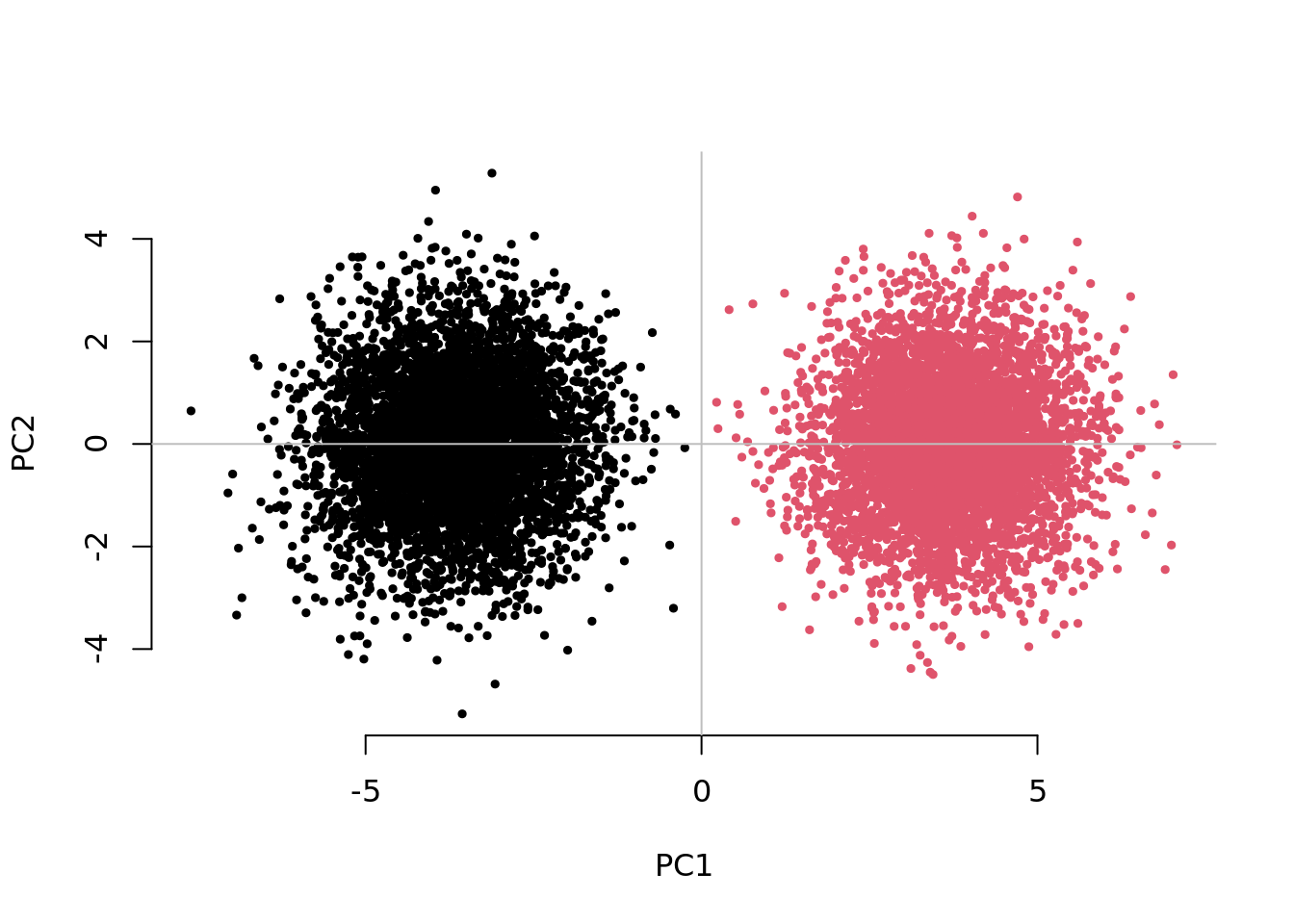
user system elapsed
55.863 0.516 56.385 testResults UnAdj PCAdj QFAM
2.1654689 0.9471238 0.9442280 This examples takes about 1 minute to run.
Question 2. Increase the number of subgroups (e.g.. g=5, g=10, g=50). What can you say about the separation between subgroups on the first two PCs? Is the adjustment for 10 PCs still sufficient to control for inflation? If not, how many PCs do you need to fit and why? What do you observe for the within-family GWAS results?
CHISQ(N=10000,M=1000,Fst=.025,vs=.05,g=5,nPC=10)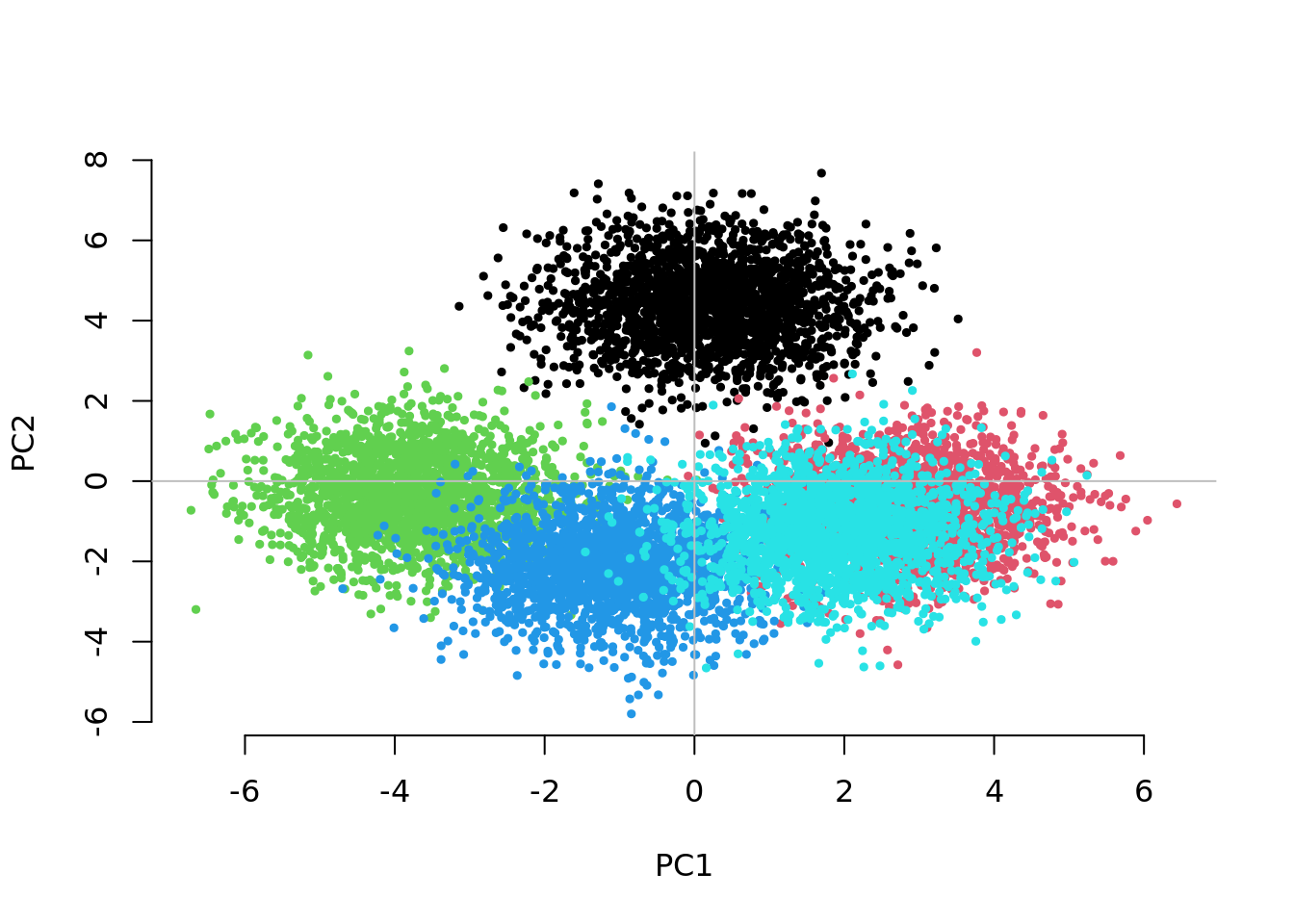
UnAdj PCAdj QFAM
1.7859034 0.9903592 0.9410527 CHISQ(N=10000,M=1000,Fst=.025,vs=.05,g=10,nPC=10)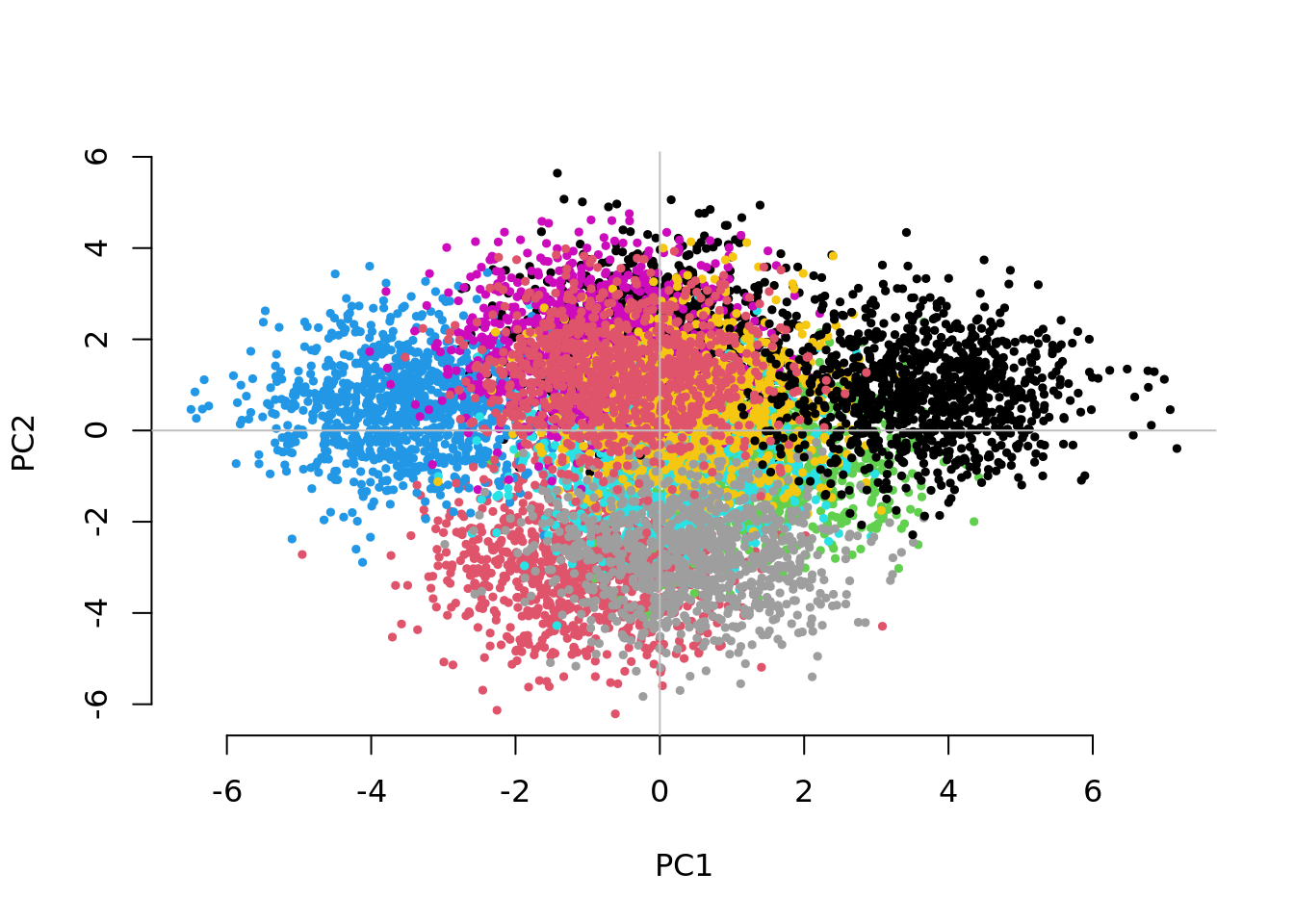
UnAdj PCAdj QFAM
3.196399 1.048966 0.982059 CHISQ(N=10000,M=1000,Fst=.025,vs=.05,g=50,nPC=10)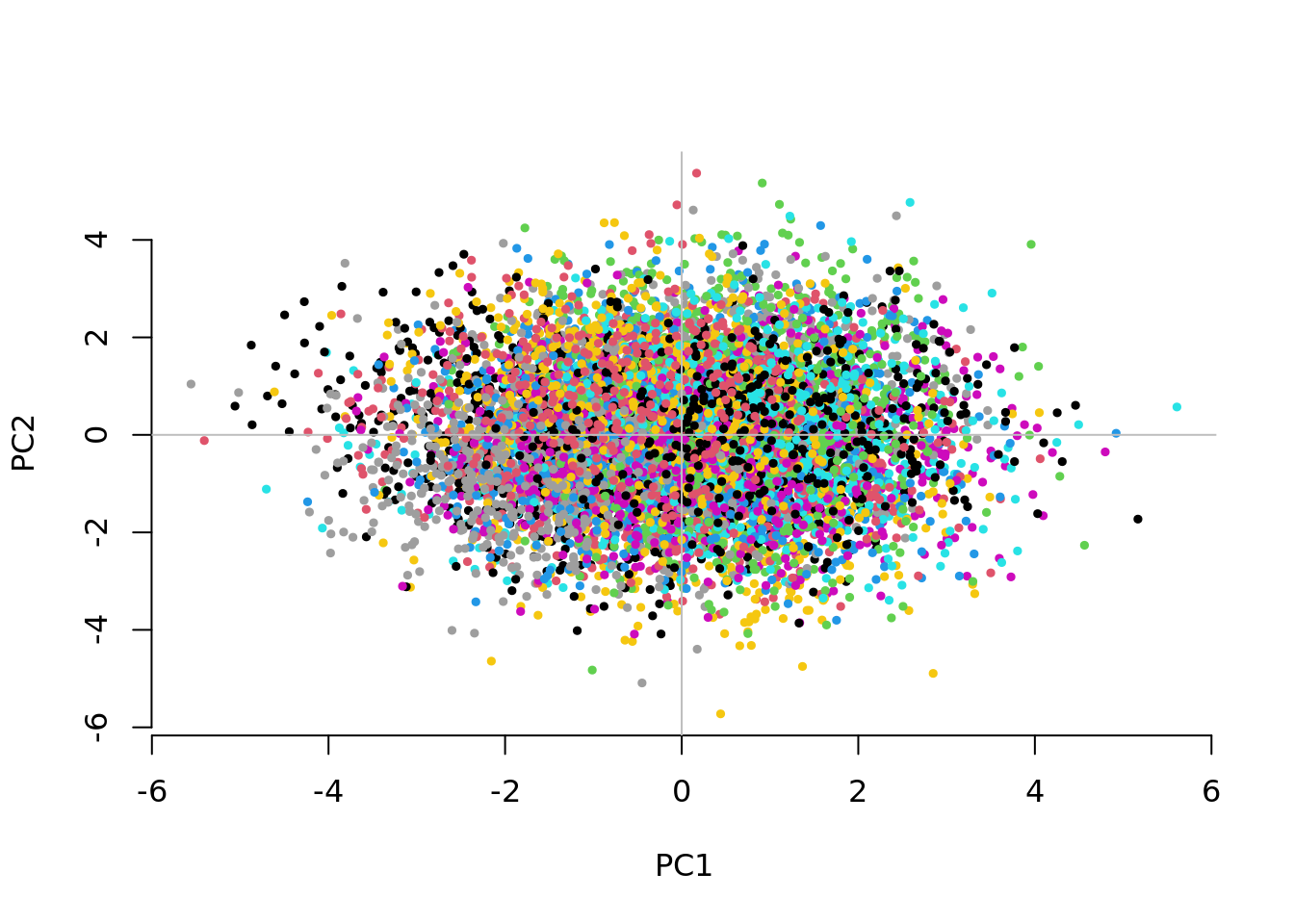
UnAdj PCAdj QFAM
1.1605441 1.1258952 0.9512546 ## Let's try fitting 50 PCs
CHISQ(N=10000,M=1000,Fst=.025,vs=.05,g=50,nPC=50)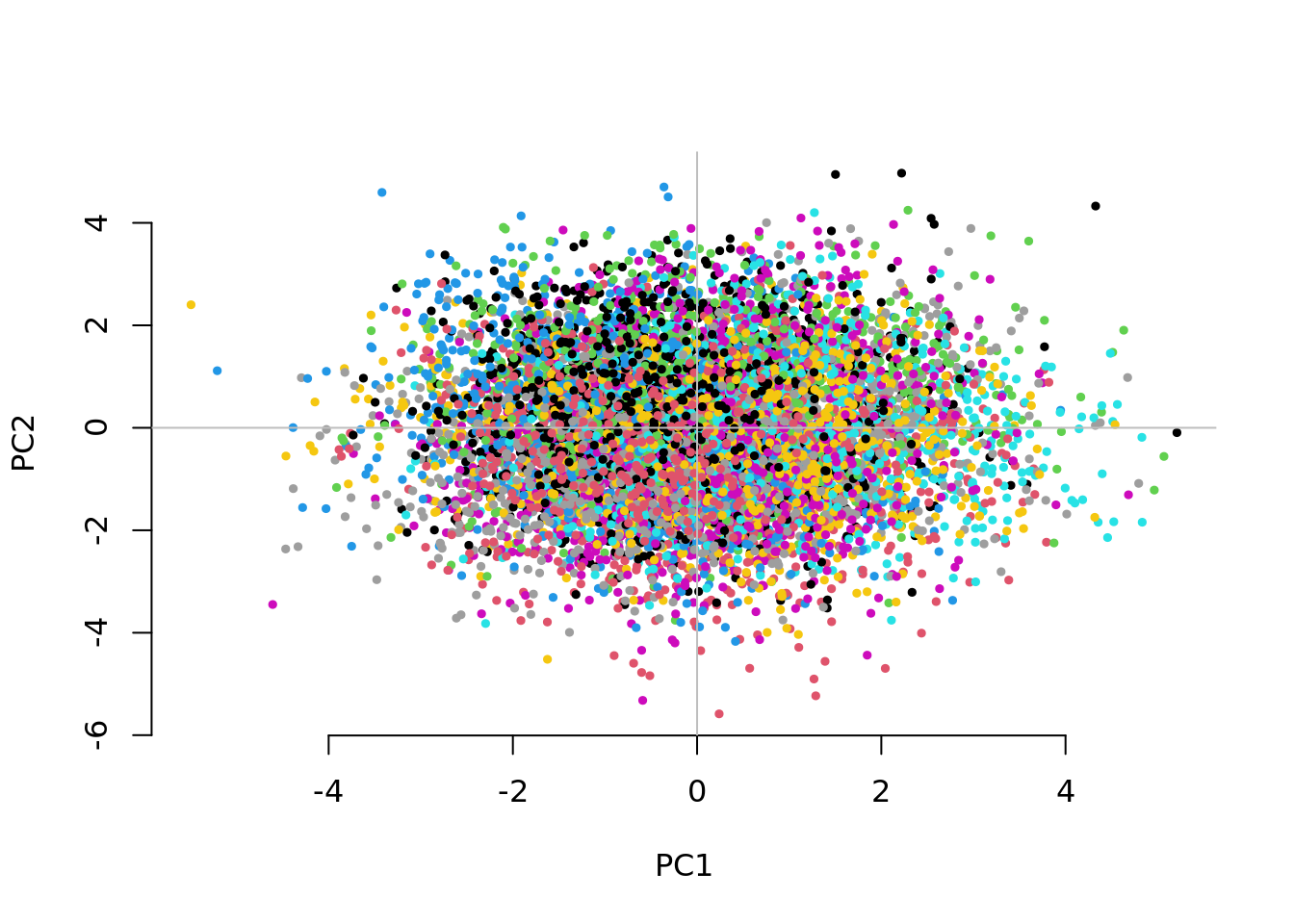
UnAdj PCAdj QFAM
1.2320150 1.1311878 0.9845612 The separation between groups along the first two PCs decreases as we increase the number of groups. Fitting the 10 PCs seems to become inefficient. Fitting as many PCs as the number of groups seems to work but also substantially increases the computational time.
Question 3. Now set Fst=0.1 (that would correspond to subgroups with different continental ancestries), vs=0.1 and g=50. Are your conclusions from Question 2 different?
CHISQ(N=10000,M=1000,Fst=.1,vs=.1,g=50,nPC=10)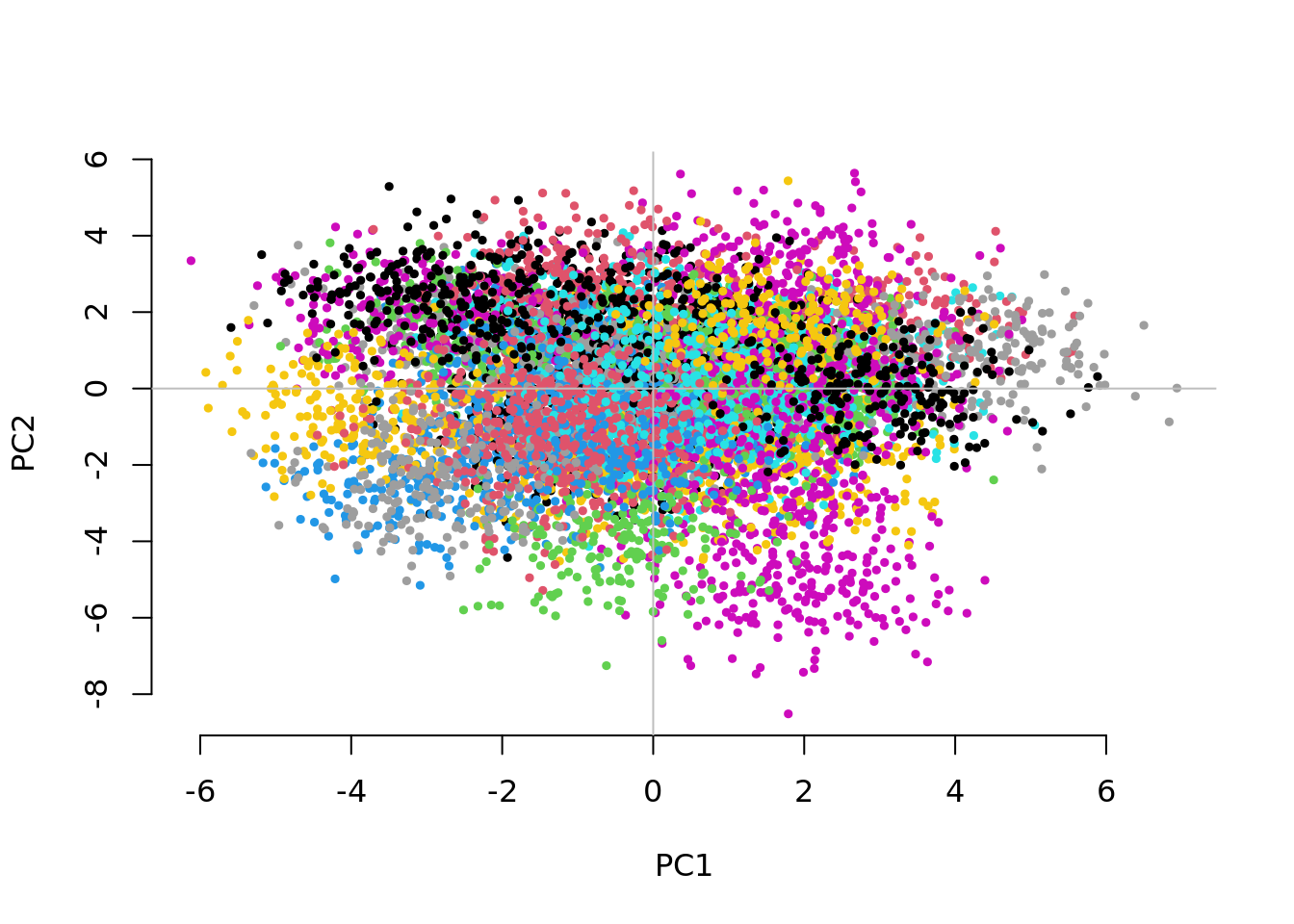
UnAdj PCAdj QFAM
3.190113 2.474966 1.001763 CHISQ(N=10000,M=1000,Fst=.1,vs=.1,g=50,nPC=50)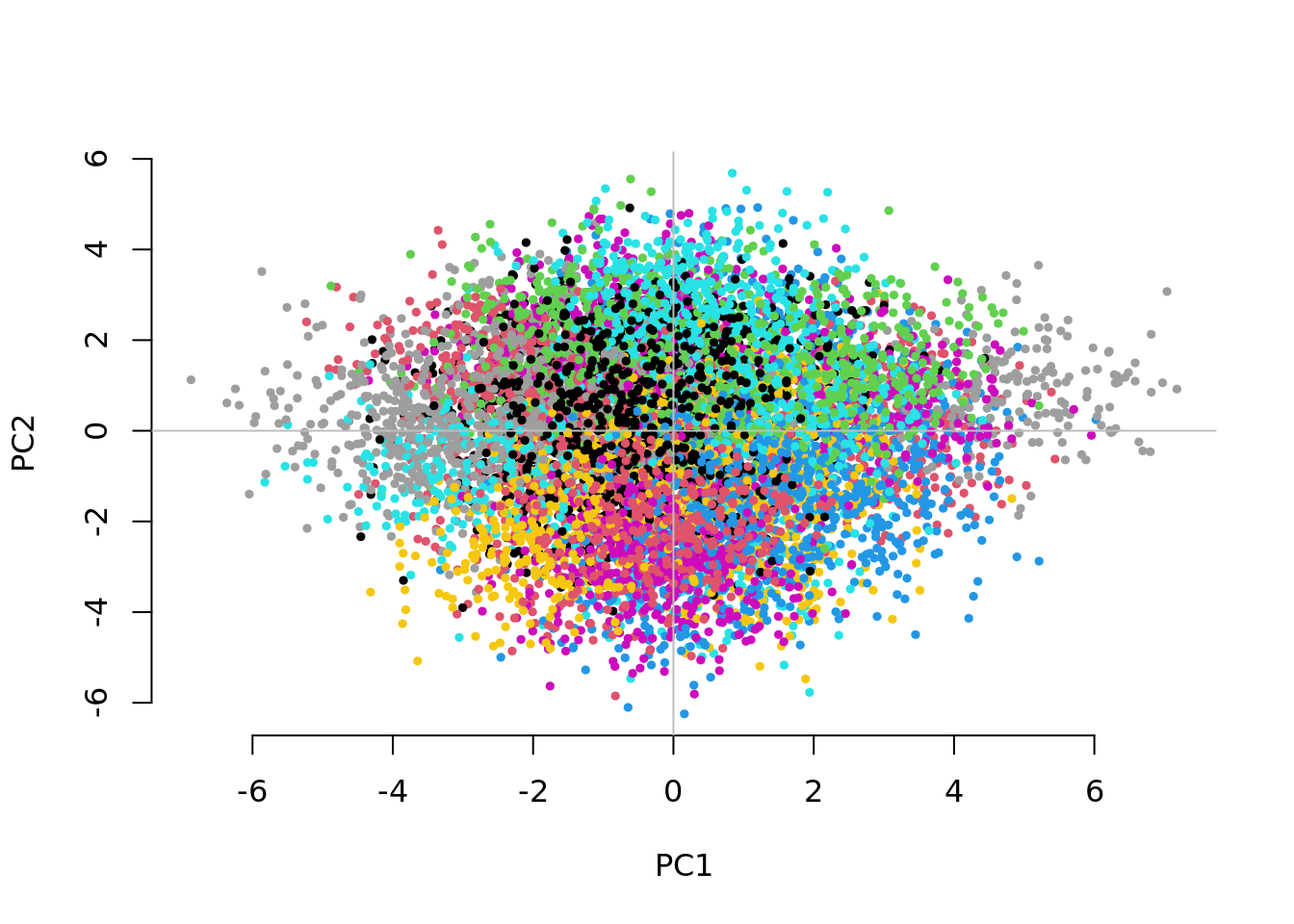
UnAdj PCAdj QFAM
3.069871 1.057847 1.014468
sessionInfo()R version 4.2.1 (2022-06-23)
Platform: x86_64-pc-linux-gnu (64-bit)
Running under: Ubuntu 22.04 LTS
Matrix products: default
BLAS: /usr/lib/x86_64-linux-gnu/blas/libblas.so.3.10.0
LAPACK: /usr/lib/x86_64-linux-gnu/lapack/liblapack.so.3.10.0
locale:
[1] LC_CTYPE=C.UTF-8 LC_NUMERIC=C LC_TIME=C.UTF-8
[4] LC_COLLATE=C.UTF-8 LC_MONETARY=C.UTF-8 LC_MESSAGES=C.UTF-8
[7] LC_PAPER=C.UTF-8 LC_NAME=C LC_ADDRESS=C
[10] LC_TELEPHONE=C LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] workflowr_1.7.0
loaded via a namespace (and not attached):
[1] Rcpp_1.0.9 highr_0.9 bslib_0.3.1 jquerylib_0.1.4
[5] compiler_4.2.1 pillar_1.7.0 later_1.3.0 git2r_0.30.1
[9] tools_4.2.1 getPass_0.2-2 digest_0.6.29 jsonlite_1.8.0
[13] evaluate_0.15 tibble_3.1.7 lifecycle_1.0.1 pkgconfig_2.0.3
[17] rlang_1.0.3 cli_3.3.0 rstudioapi_0.13 yaml_2.3.5
[21] xfun_0.31 fastmap_1.1.0 httr_1.4.3 stringr_1.4.0
[25] knitr_1.39 sass_0.4.1 fs_1.5.2 vctrs_0.4.1
[29] rprojroot_2.0.3 glue_1.6.2 R6_2.5.1 processx_3.7.0
[33] fansi_1.0.3 rmarkdown_2.14 callr_3.7.0 magrittr_2.0.3
[37] whisker_0.4 ps_1.7.1 promises_1.2.0.1 htmltools_0.5.2
[41] ellipsis_0.3.2 httpuv_1.6.5 utf8_1.2.2 stringi_1.7.6
[45] crayon_1.5.1