Solution for Practical 5: Conditional and Joint Analysis (COJO)
Summer Institute of Statical Genetics (Module 15)
2022-07-26
Last updated: 2022-07-26
Checks: 7 0
Knit directory: SISG2022_Association_Mapping/
This reproducible R Markdown analysis was created with workflowr (version 1.7.0). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20220530) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.
The results in this page were generated with repository version db25cfb. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.
Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:
Ignored files:
Ignored: analysis/.DS_Store
Ignored: analysis/.Rhistory
Ignored: code/.Rhistory
Ignored: data/.DS_Store
Ignored: lectures/.DS_Store
Untracked files:
Untracked: GWAS.ma
Untracked: analysis/.index.Rmd.swp
Untracked: analysis/SISGM15_prac6Solution.Rmd
Untracked: analysis/SISGM15_prac9Solution.Rmd
Untracked: analysis/Session07_practical_Key.Rmd
Untracked: analysis/Session08_practical_Key.Rmd
Untracked: causals.snplist
Untracked: ldRef.bed
Untracked: ldRef.bim
Untracked: ldRef.fam
Untracked: ldRef.log
Untracked: ldRef.map
Untracked: ldRef.ped
Untracked: test1.cma.cojo
Untracked: test1.jma.cojo
Untracked: test1.ldr.cojo
Untracked: test1.log
Untracked: test2.cma.cojo
Untracked: test2.jma.cojo
Untracked: test2.ldr.cojo
Untracked: test2.log
Untracked: test3.cma.cojo
Untracked: test3.jma.cojo
Untracked: test3.ldr.cojo
Untracked: test3.log
Untracked: test4.cma.cojo
Untracked: test4.jma.cojo
Untracked: test4.ldr.cojo
Untracked: test4.log
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the repository in which changes were made to the R Markdown (analysis/SISGM15_prac5Solution.Rmd) and HTML (docs/SISGM15_prac5Solution.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | db25cfb | Joelle Mbatchou | 2022-07-26 | add key to S5 |
This practical runs on the SISG2022 server.
This practical aims at
Familiarizing you with GCTA-COJO (or COJO in short)
Exploring different factors influencing COJO outcomes
The practical is run in R but uses the R function system() to run PLINK and GCTA from the terminal. If you have PLINK and GCTA installed on your own computer then you could also run it locally if your prefer. In that case you’d need to update a few links provided below.
The COJO algorithm is not designed for fine-mapping per se. However, many of the challenges illustrated and discussed in this practical are relevant for any method using external linkage disequilibrium (LD) reference.
Part I: the data
We provide an R code that simulates a 1 Mb long chromosome with M=2000 SNPs organized within 20 LD blocks. Each block contains 100 SNPs, among which 5 causal variants. SNPs within a block are numbered between 1 and 100, such that the squared correlation \(r^2_{i_{k}j_{k}}\) of allele counts at SNP \(i_k\) and \(j_k\) within LD block \(k\) is
\[ r^2_{i_{k}j_{k}} = \rho_k^{2|i_k-j_k|} \]
LD blocks are characterized by the parameters \(\rho^2_k\), which varies from 0.1 (when \(k=1\); low LD locus) to 0.9 (when \(k=20\); high LD locus).
The code below generates the LD correlation structure between SNPs in each block.
Run the following commands
set.seed(28072022)
nblocks <- 20
rhos <- sqrt(seq(0.1,0.9,len=nblocks))
m <- 100 # number of SNPs per LD block
mcBlock <- 5 # number of causals LD per block
M <- m * nblocks
R <- matrix(0,nrow=M,ncol=M)
icausal <- c()
for(k in 1:nblocks){
l <- ((k-1)*m + 1):(k*m);
R[l,l] <- outer(1:m,1:m,FUN=function(i,j) rhos[k]^abs(i-j))
icausal <- c(icausal,sample(l,mcBlock))
}The figure code and figure below shows the LD correlation matrix for SNPs the 20-th LD block (\(\rho^2_{20}=0.9\))
k=20
l=((k-1)*m + 1):(k*m)
heatmap(R[l,l],Rowv=NA,Colv=NA)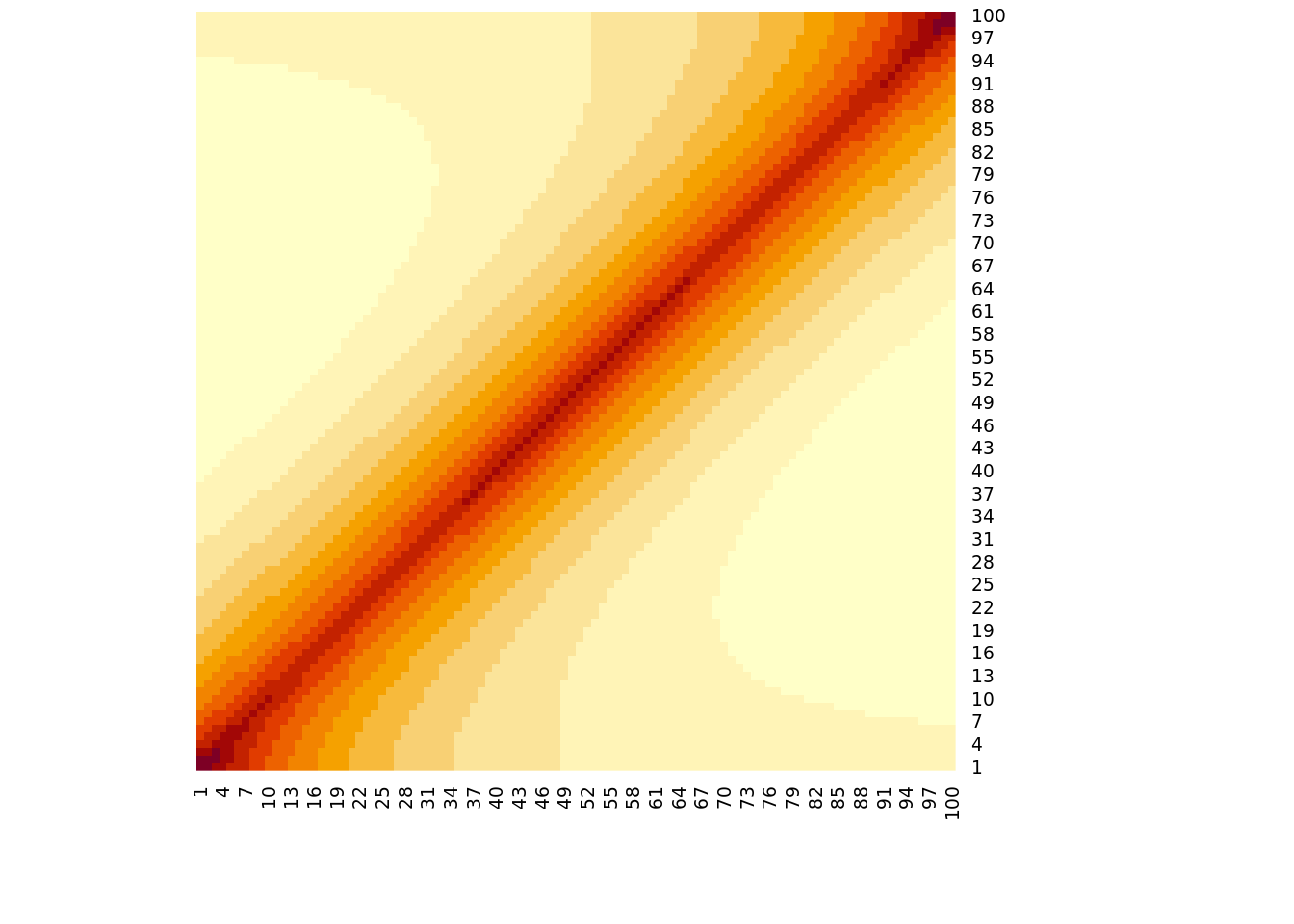
print("Extract of LD structure for 20-th LD block")[1] "Extract of LD structure for 20-th LD block"print( R[l,l][1:5,1:5] ) [,1] [,2] [,3] [,4] [,5]
[1,] 1.0000000 0.9486833 0.9000000 0.8538150 0.8100000
[2,] 0.9486833 1.0000000 0.9486833 0.9000000 0.8538150
[3,] 0.9000000 0.9486833 1.0000000 0.9486833 0.9000000
[4,] 0.8538150 0.9000000 0.9486833 1.0000000 0.9486833
[5,] 0.8100000 0.8538150 0.9000000 0.9486833 1.0000000Run the following commands
chr <- 10 # Chromosome number
pos <- 1234557 + sort(sample(0:1e6,M)) # Random Position for SNPs
a1a2 <- do.call("rbind",lapply(1:M,function(j) sample(c("A","C","G","T"),2))) # alleles
snps <- paste0("SNP",1:M) # SNP ID
ldblock <- rep(1:nblocks,each=m) # LD block ID
names(ldblock) <- snpsThe R code below generates and shows the LD score of each SNP on the chromosome (x-axis: genomic position in Mb; y-axis: LD score)
Cols <- sample(colors(),nblocks)
ldscores <- diag(crossprod(R))
plot(pos/1e6,ldscores,pch=19,col=Cols[ldblock],
axes=FALSE,xlab="Genomic Position (Mb)",
ylab="LD scores")
axis(1);axis(2)
legend("topleft",legend=paste0("Block #",1:nblocks),
box.lty=0,pch=19,cex=0.5,col=Cols)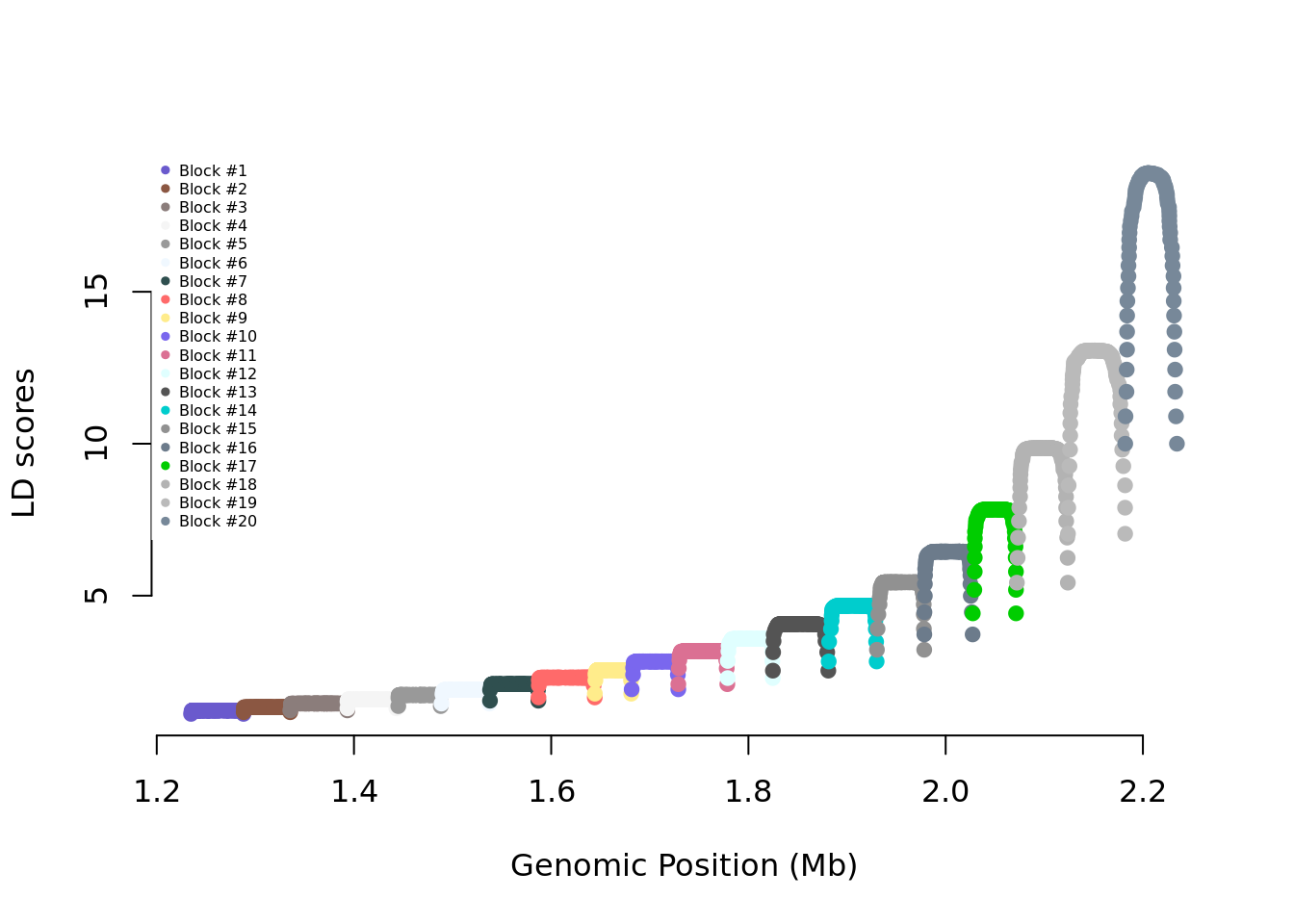
cat(paste0("mean LD score = ",round(mean(ldscores),3),
" - SD LD score = ",round(sd(ldscores),3)))mean LD score = 4.598 - SD LD score = 4.13Run the following commands. This is a function to generate genotypes corresponding to the specified LD structure. For simplicity, we simulate all SNPs with an allele frequency equal to 0.5.
library(MASS)
simGeno <- function(R,n){
z1 <- do.call("cbind",lapply(1:nblocks,function(i){
l <- ((i-1)*m + 1):(i*m)
mvrnorm(n=n,mu=rep(0,m),Sigma = R[l,l])
}))
z2 <- do.call("cbind",lapply(1:nblocks,function(i){
l <- ((i-1)*m + 1):(i*m)
mvrnorm(n=n,mu=rep(0,m),Sigma = R[l,l])
}))
x <- (z1>0) + (z2>0)
return(x)
}Run the following commands to genarate genotypes and phenotypes of GWAS participants. GWAS sample size is Ngwas=100000
Ngwas <- 5e4
## Simulate genotypes
Xgwas <- simGeno(n = Ngwas,R)
## Simulate phenotype
mc <- length(icausal) # total number of causal variants
q2 <- 0.01 #variance explained by all SNPs on the chromosome
b <- rnorm(n=mc,mean=0,sd=sqrt(q2/mc))
g <- sqrt(2)*c((Xgwas[,icausal]-1)%*%b)
e <- rnorm(n=Ngwas,mean=0,sd=sqrt(1-q2))
Ygwas <- g + e
## Running GWAS
var_x <- apply(Xgwas,2,var)
beta <- cov(Xgwas,Ygwas) / var_x # estimated regression coefficients
se <- sqrt( (var(Ygwas) - beta*beta*var_x)/((Ngwas-2)*var_x) ) # standard errors
pval <- 2 * pt(q=abs(beta/se),df=Ngwas-2,lower.tail = F) # T-distribution
## GWAS data - COJO format
gwas <- cbind.data.frame(SNP=snps,A1=a1a2[,1],A2=a1a2[,2],
Freq=colMeans(Xgwas)/2,beta=beta,
se=se,P=pval,N=Ngwas)
print(head(gwas,3)) SNP A1 A2 Freq beta se P N
1 SNP1 C T 0.49772 -0.009919254 0.006328504 0.11702916 50000
2 SNP2 T C 0.49824 -0.001585635 0.006315480 0.80176012 50000
3 SNP3 C A 0.50110 0.011048179 0.006358965 0.08231961 50000# folder where to store the data
# default is ".", i.e. current directory
# this can be changed
datPath <- "."
write.table(gwas,paste0(datPath,"/GWAS.ma"),
quote=FALSE,row.names=FALSE,
col.names=TRUE,sep="\t")
causals <- snps[icausal]
write(causals,paste0(datPath,"/causals.snplist")) ## list of causal SNPsRun the following commands to simulate a LD reference (i.e., set of genotypes in PLINK format) from the same population.
## Set path for PLINK
plink <- "/data/SISG2022M15/exe/plink"
## Simulate and write LD ref
simLDref <- function(Nldref){
Xldref <- simGeno(n = Nldref,R)
refGeno <- t(sapply(1:M,function(j) {
c(paste0(a1a2[j,1],"\t",a1a2[j,1]),
paste0(a1a2[j,1],"\t",a1a2[j,2]),
paste0(a1a2[j,2],"\t",a1a2[j,2]))
}))
ped <- do.call("cbind",lapply(1:M,function(j){
refGeno[j,1+Xldref[,j]]}
))
## fam file
iid <- paste0("IID",1:Nldref)
fid <- iid
pid <- rep(0,Nldref)
mid <- rep(0,Nldref)
sex <- sample(1:2,Nldref,replace=TRUE)
pheno <- rep(-9,Nldref)
fam <- cbind.data.frame(fid,iid,pid,mid,sex,pheno)
## ped/geno
mapData <- cbind.data.frame(chr,snps,0,pos)
pedData <- cbind.data.frame(fam,ped)
write.table(mapData,paste0(datPath,"/ldRef.map"),
quote=FALSE,row.names=FALSE,col.names=FALSE,sep="\t")
write.table(pedData,paste0(datPath,"/ldRef.ped"),
quote=FALSE,row.names=FALSE,col.names=FALSE,sep="\t")
system(paste0(plink," --file ldRef --make-bed --out ldRef"))
}
simLDref(Nldref = 5000)Part II: running COJO
If you have run all the commands above then the following files must be available in your current directory. To check type the following command in the terminal.
ls -lt GWAS.ma
ls -lt ldRef.*-rw-rw-r-- 1 joelle.mbatchou joelle.mbatchou 167371 Jul 26 16:04 GWAS.ma
-rw-rw-r-- 1 joelle.mbatchou joelle.mbatchou 2500003 Jul 26 16:04 ldRef.bed
-rw-rw-r-- 1 joelle.mbatchou joelle.mbatchou 48893 Jul 26 16:04 ldRef.bim
-rw-rw-r-- 1 joelle.mbatchou joelle.mbatchou 122786 Jul 26 16:04 ldRef.fam
-rw-rw-r-- 1 joelle.mbatchou joelle.mbatchou 974 Jul 26 16:04 ldRef.log
-rw-rw-r-- 1 joelle.mbatchou joelle.mbatchou 40122786 Jul 26 16:04 ldRef.ped
-rw-rw-r-- 1 joelle.mbatchou joelle.mbatchou 40893 Jul 26 16:04 ldRef.mapYou can now run COJO. Either from the terminal
GCTA=/data/SISG2022M15/exe/gcta64_v1.94
${GCTA} --bfile ldRef --cojo-file GWAS.ma --chr 10 --cojo-slct --cojo-p 2.5e-5 --out test1*******************************************************************
* Genome-wide Complex Trait Analysis (GCTA)
* version 1.94.0 beta Linux
* (C) 2010-present, Jian Yang, The University of Queensland
* Please report bugs to Jian Yang <jian.yang.qt@gmail.com>
*******************************************************************
Analysis started at 16:04:29 UTC on Tue Jul 26 2022.
Hostname: si2022-compute
Accepted options:
--bfile ldRef
--cojo-file GWAS.ma
--chr 10
--cojo-slct
--cojo-p 2.5e-05
--out test1
Reading PLINK FAM file from [ldRef.fam].
5000 individuals to be included from [ldRef.fam].
Reading PLINK BIM file from [ldRef.bim].
2000 SNPs to be included from [ldRef.bim].
2000 SNPs on chromosome 10 are included in the analysis.
Reading PLINK BED file from [ldRef.bed] in SNP-major format ...
Genotype data for 5000 individuals and 2000 SNPs to be included from [ldRef.bed].
Reading GWAS summary-level statistics from [GWAS.ma] ...
GWAS summary statistics of 2000 SNPs read from [GWAS.ma].
Phenotypic variance estimated from summary statistics of all 2000 SNPs: 1.00122 (variance of logit for case-control studies).
Matching the GWAS meta-analysis results to the genotype data ...
Calculating allele frequencies ...
2000 SNPs are matched to the genotype data.
Calculating the variance of SNP genotypes ...
Performing stepwise model selection on 2000 SNPs to select association signals ... (p cutoff = 2.5e-05; collinearity cutoff = 0.9)
(Assuming complete linkage equilibrium between SNPs which are more than 10Mb away from each other)
5 associated SNPs have been selected.
10 associated SNPs have been selected.
Finally, 12 associated SNPs are selected.
Performing joint analysis on all the 12 selected signals ...
Saving the 12 independent signals to [test1.jma.cojo] ...
Saving the LD structure of 12 independent signals to [test1.ldr.cojo] ...
Saving the conditional analysis results of 1988 remaining SNPs to [test1.cma.cojo] ...
(0 SNPs eliminated by backward selection and 0 SNPs filtered by collinearity test are not included in the output)
Analysis finished at 16:04:31 UTC on Tue Jul 26 2022
Overall computational time: 2.88 sec.or from R (calling terminal using the system() command)
gcta <- "/data/SISG2022M15/exe/gcta64_v1.94"
system(paste0(gcta," --bfile ldRef ",
"--cojo-file GWAS.ma --chr 10 ",
"--cojo-slct --cojo-p 2.5e-5 --out test1"))Question 1. How many SNPs are detected? How many of those are causal SNPs? (Note that you can obtain causal SNPs in your currrent R session as causals = snps[icausal], or in the file named causals.snplist).
The number of SNPs detected by COJO is displayed in the log file “Saving the 10 independent signals to [test1.jma.cojo].” and corresponds to the number of rows (minus one) in the *.jma.cojo file. Here, 10 SNPs were detected…
cojo1 <- read.table("test1.jma.cojo",h=T,stringsAsFactors = FALSE) ## Read COJO results
print( table(cojo1$SNP%in%snps[icausal]) ) ## Count how many are causal
FALSE TRUE
1 11 …including 10 causal variants.
Question 2. Regenerate LD reference data with a lower sample size Nldref=2000, 1000 and 500 and rerun 1). What do you observe? Are all LD blocks affected the same?
Let us focus on the smallest LD reference Nldref=2000. We modify and re-run some of the R commands given above…
simLDref(Nldref = 500)
system(paste0(gcta," --bfile ldRef ",
"--cojo-file GWAS.ma --chr 10 ",
"--cojo-slct --cojo-p 2.5e-5 --out test2"))
cojo2 <- read.table("test2.jma.cojo",h=T,stringsAsFactors = FALSE) ## Read COJO results
print( table(cojo2$SNP%in%snps[icausal]) ) ## Count how many are causal
FALSE TRUE
215 24 We can see that 246 SNPs are now detected but only 23 of them are causal. To see if all LD blocks are affected the same, we can visualize the number of COJO SNPs (here mostly false positives) in each LD block using (for example) the following command.
barplot(table(ldblock[cojo2$SNP]),ylab="# COJO SNPs in each LD block",
xlab="LD blocks (1: low LD; 20: high LD)")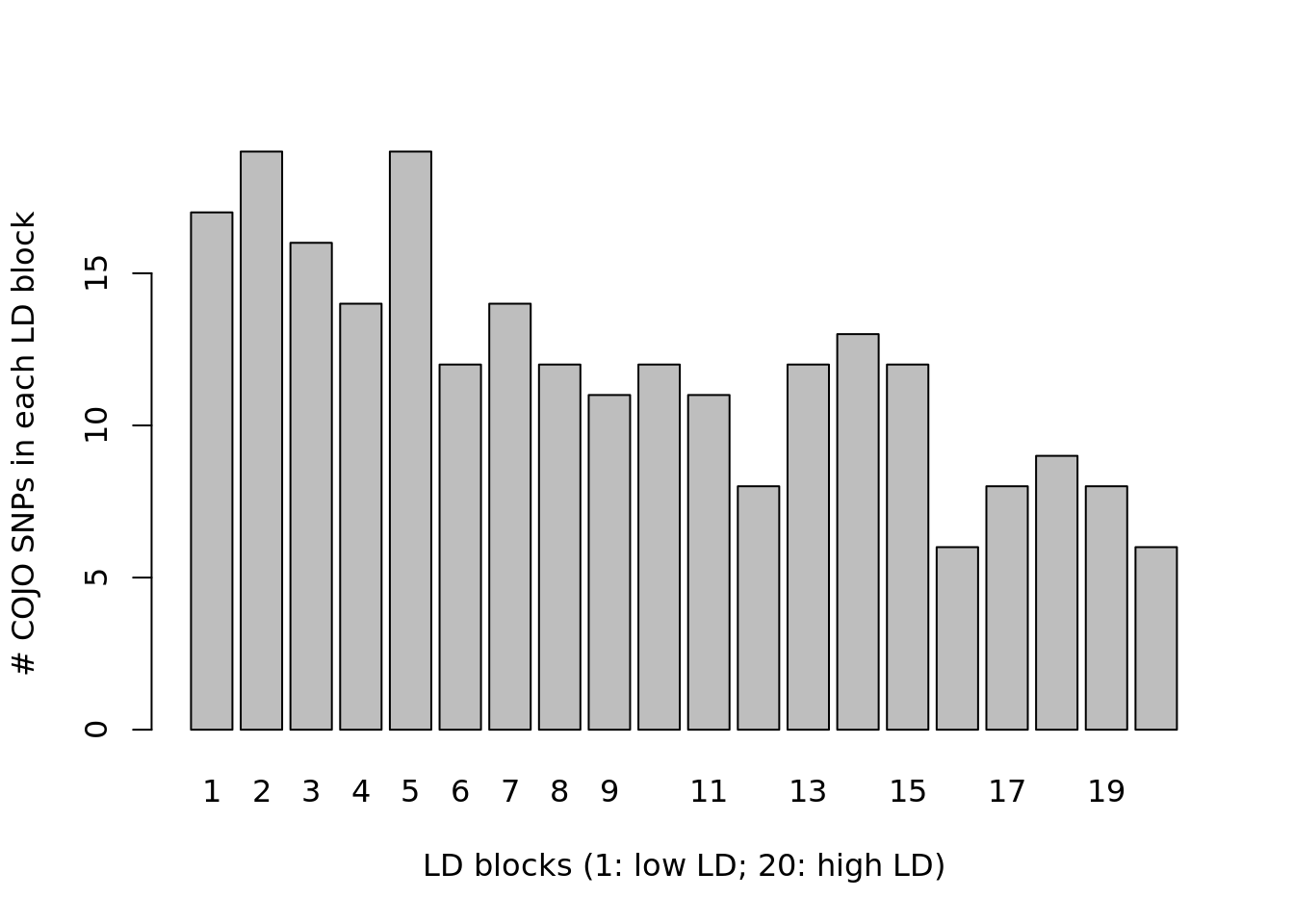
Conclusion: the inflation is larger in low LD blocks.
Question 3. Set the variance explained by SNPs on the chromosome to 3% (q2=0.03) and re-run 1) and 2). What can you conclude regarding the number of SNPs detected and the proportion of non-causal SNPs detected?
Conclusion: the inflation of false positives observed with small LD reference is larger when the signal (\(q^2\)) is strong.
Part III: fixing COJO?
There is no simple way to fix the inflation of false positive observed when the LD reference is too small. As a rule of thumb, Yang et al. (GCTA website) recommend using sample sizes of at least 4000. Nevertheless, we observe that using a more stringent threshold for detecting collinearity might help.
Question 4. Set the variance explained by SNPs on the chromosome to 3% (q2=0.03) and the size of the LD reference to 1000. Re-run COJO adding the following flag --cojo-collinear 0.1. Quantify the improvement in the number of false positives.
q2 <- 0.03 #variance explained by all SNPs on the chromosome
b <- rnorm(n=mc,mean=0,sd=sqrt(q2/mc))
g <- sqrt(2)*c((Xgwas[,icausal]-1)%*%b)
e <- rnorm(n=Ngwas,mean=0,sd=sqrt(1-q2))
Ygwas <- g + e
beta <- cov(Xgwas,Ygwas) / var_x # estimated regression coefficients
se <- sqrt( (var(Ygwas) - beta*beta*var_x)/((Ngwas-2)*var_x) ) # standard errors
pval <- 2 * pt(q=abs(beta/se),df=Ngwas-2,lower.tail = F) # T-distribution
gwas <- cbind.data.frame(SNP=snps,A1=a1a2[,1],A2=a1a2[,2],
Freq=colMeans(Xgwas)/2,beta=beta,
se=se,P=pval,N=Ngwas)
print(head(gwas,3)) SNP A1 A2 Freq beta se P N
1 SNP1 C T 0.49772 0.001225852 0.006326721 0.8463663 50000
2 SNP2 T C 0.49824 -0.003415884 0.006313533 0.5884813 50000
3 SNP3 C A 0.50110 -0.001948620 0.006357205 0.7592089 50000write.table(gwas,paste0(datPath,"/GWAS.ma"),
quote=FALSE,row.names=FALSE,
col.names=TRUE,sep="\t")
## Simulate LD reference and run COJO
simLDref(Nldref = 1000)
system(paste0(gcta," --bfile ldRef ",
"--cojo-file GWAS.ma --chr 10 ",
"--cojo-slct --cojo-p 2.5e-5 --out test3"))
cojo3 <- read.table("test3.jma.cojo",h=T,stringsAsFactors = FALSE)
print( table(cojo3$SNP%in%snps[icausal]) ) ## Count how many are causal
FALSE TRUE
37 32 system(paste0(gcta," --bfile ldRef ",
"--cojo-file GWAS.ma --chr 10 --cojo-collinear 0.05 ",
"--cojo-slct --cojo-p 2.5e-5 --out test4"))
cojo4 <- read.table("test4.jma.cojo",h=T,stringsAsFactors = FALSE)
print( table(cojo4$SNP%in%snps[icausal]) ) ## Count how many are causal
FALSE TRUE
10 23 Conclusion: using a more stringent collinearity threshold can reduce the proportion of false positives.
sessionInfo()R version 4.2.1 (2022-06-23)
Platform: x86_64-pc-linux-gnu (64-bit)
Running under: Ubuntu 22.04 LTS
Matrix products: default
BLAS: /usr/lib/x86_64-linux-gnu/blas/libblas.so.3.10.0
LAPACK: /usr/lib/x86_64-linux-gnu/lapack/liblapack.so.3.10.0
locale:
[1] LC_CTYPE=C.UTF-8 LC_NUMERIC=C LC_TIME=C.UTF-8
[4] LC_COLLATE=C.UTF-8 LC_MONETARY=C.UTF-8 LC_MESSAGES=C.UTF-8
[7] LC_PAPER=C.UTF-8 LC_NAME=C LC_ADDRESS=C
[10] LC_TELEPHONE=C LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] MASS_7.3-57 workflowr_1.7.0
loaded via a namespace (and not attached):
[1] Rcpp_1.0.9 highr_0.9 bslib_0.3.1 jquerylib_0.1.4
[5] compiler_4.2.1 pillar_1.7.0 later_1.3.0 git2r_0.30.1
[9] tools_4.2.1 getPass_0.2-2 digest_0.6.29 jsonlite_1.8.0
[13] evaluate_0.15 tibble_3.1.7 lifecycle_1.0.1 pkgconfig_2.0.3
[17] rlang_1.0.3 cli_3.3.0 rstudioapi_0.13 yaml_2.3.5
[21] xfun_0.31 fastmap_1.1.0 httr_1.4.3 stringr_1.4.0
[25] knitr_1.39 sass_0.4.1 fs_1.5.2 vctrs_0.4.1
[29] rprojroot_2.0.3 glue_1.6.2 R6_2.5.1 processx_3.7.0
[33] fansi_1.0.3 rmarkdown_2.14 callr_3.7.0 magrittr_2.0.3
[37] whisker_0.4 ps_1.7.1 promises_1.2.0.1 htmltools_0.5.2
[41] ellipsis_0.3.2 httpuv_1.6.5 utf8_1.2.2 stringi_1.7.6
[45] crayon_1.5.1